동적 계획법
동적 : 프로그램이 실행되면서 필요한 메모리를 할당하는 기법을 의미한다.
큰 문제를 작은 문제로 나누어 풀고 결과를 저장하고 재활용하는 알고리즘이다
대표적인 문제로 피보나치의 수 f(n) = f(n-1) + f(n-2) 가 있다.
DP의 사용 조건
1. 반복되는 부분문제 (Overlapping Subproblems)
부분문제가 반복되지 않는다 = 재사용이 불가능 하니 DP알고리즘을 사용할수 없다.

피보나치의 수에서는 다음과 같이 반복되는 항이 있어 재활용이 가능하다.
2. 최적부분 구조 (Optimal Substructure)
구하려는 문제(큰 문제) 정답을 작은 문제 최적의 합으로 구할수가 있다.
큰 문제 f(n) 는 작은 문제 f(n-1) + f(n-2) 로 계산이 가능하다.
재귀함수와 DP의 차이점
재귀함수를 단순히 사용하면 이미 계산한 작은 문제들이 여러번 반복된다.
f(n) = f(n-1) + f(n-2) > 2 x f(n-2) > 2^2 x f(n-4) ... >= 2^n/2
( 무조건 f(n-1)이 f(n-2) 이상이므로 )
즉 Big O 표기법 특징인 상수항 무시로 O(n^2) 시간복잡도를 가진다.
6번째 항 계산을 예로들면
f(6) = f(5)+f(4) , f(5) = f(4) + f(3) , f(4) =f(3) + f(2) ... 이미 계산한 항을 반복계산한다.
DP는 아래 피보니치의 수 코드를 보면 계산한 값들을 memo에 저장해두고
재귀함수로 호출하는 수가 memo에 있으면 그 수를 가져오는 방법으로 계산을 줄인다.

f(n)= f(n-1) + c= f(n-2) + c + c = ... =f(1) + (n-1)c = cn
따라서 두번씩 계산되지 않기 때문에 시간 복잡도가 O(f(n) 즉 O(n) 으로 줄게된다
//Top - down 방식
public class B2747 {
static int N;
static int[] memo;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
memo = new int[N+1];
System.out.println(fibonacci(N));
}
static public int fibonacci(int n) {
if (n <= 1)
return n;
else if (n == 2)
return 1;
else {
// 이미 있는값은 리턴
if (memo[n] > 0)
return memo[n];
memo[n] = fibonacci(n-1) + fibonacci(n-2);
return memo[n];
}
}
}
구현방법
2747번: 피보나치 수
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가
www.acmicpc.net
1. Top-Dwon
시작점이 DP[0] 이 아니라 구하려는 값 DP[n]에서 부터 시작하여 아래로 타고내려가며 DP[0] 까지 간 후
재귀를 통해 저장된 값을 재활용하여 DP[n]을 구하는 방법이다.
이전 계산값을 위 코드에서는 memo에 저장하고 꺼내보는 방식으로 반복을 피한다.
( memo[n]>0 이미 n번에 값이 있으면 return )
위 피보니치 수를 구하는 코드에서 사용한 방법이다
2. Bottom-Up
public class B2747 {
static int[] memo;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
memo = new int[N+1];
System.out.println(fibonacci(N));
}
static public int fibonacci(int n) {
if(n<=1) return n;
memo[1] = 1;
memo[2] = 1;
for (int i = 3; i < n+1; i++) {
memo[i] = memo[i-1] + memo[i-2];
}
return memo[n];
}
}DP[0]에서 시작해서 DP[n]값을 for문과 점화식으로 구하는 방법이다.
memo에 저장한 값을 가져와서 f(n)을 구하는 것을 볼 수 있다.
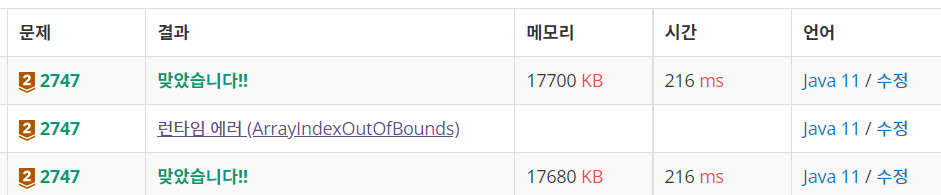
아래가 상향식 결과값이고 위가 하향식 결과값이다.
(중간에 런타임 에러는 입력값 1과 2의 예외처리를 해주지 않아서 런타임 에러가 났다...)
참고한 글
알고리즘 - Dynamic Programming(동적 계획법)
1. 개요 DP, 즉 다이나믹 프로그래밍(또는 동적 계획법)은 기본적인 아이디어로 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것으
hongjw1938.tistory.com
[자료구조] 피보나치 수열의 시간 복잡도 완벽히 이해하기
목표 피보나치 수열의 시간 복잡도(Time Complexity)에 대해서 이해해보도록 하겠습니다. 목차 클릭하면 해당 목차로 이동합니다. 피보나치(Fibonacci) 수열이란? 피보나치 수열을 구하는 알고리즘 피
chanos.tistory.com
[C/C++]재귀함수를 이용한 피보나치수열이 O(n)의 시간 복잡도를 가지는 코드
[1]재귀함수를 통한 구현 우선 윤성우의 열혈 자료구조 교재 코드를 활용하여 사용자에게 값을 입력받아 재귀함수를 이용한 피보나치수열을 작성하였다. #include int Fibo(int n) { if(n == 1) //피보나치
dev-woody.tistory.com
'수업 & 공부' 카테고리의 다른 글
| lambda (0) | 2022.10.01 |
|---|---|
| Wrapper Class란 (0) | 2022.09.29 |
| Java - Collection (0) | 2022.09.29 |
| 시간 복잡도 관련 참고할 글 (0) | 2022.08.25 |
| Spring boot Request DTO 에 null값 (0) | 2022.03.01 |

